二分查找的实现细节

发表于 2018-03-10，预计阅读时间 2 分钟

前言

最近留意到关于实现二分查找算法（Binary Search Algorithm）的一个小提醒，内容大致意思是：尽管算法思想很简单，但我们在正确实现二分查找的时候，仍需注意一下关于算法退出条件和中间值计算的相关细节。

本篇文章简单介绍二分查找算法，围绕相关的实现细节问题，做些浅显的分析。

简单介绍

在计算机科学中，二分查找也被称为折半查找、对数查找，是一种在有序数组中查找目标元素的搜索算法。

二分查找会将目标元素与数组中间元素进行比较，若不相等，则目标元素不存在的半段数组会被淘汰，并且查询会在目标元素存在的半段数组中继续进行，直到比较成功为止。如果查询以空数组为结束，则表示目标元素不存在。

一次二分查找的具体过程可以参考下图：

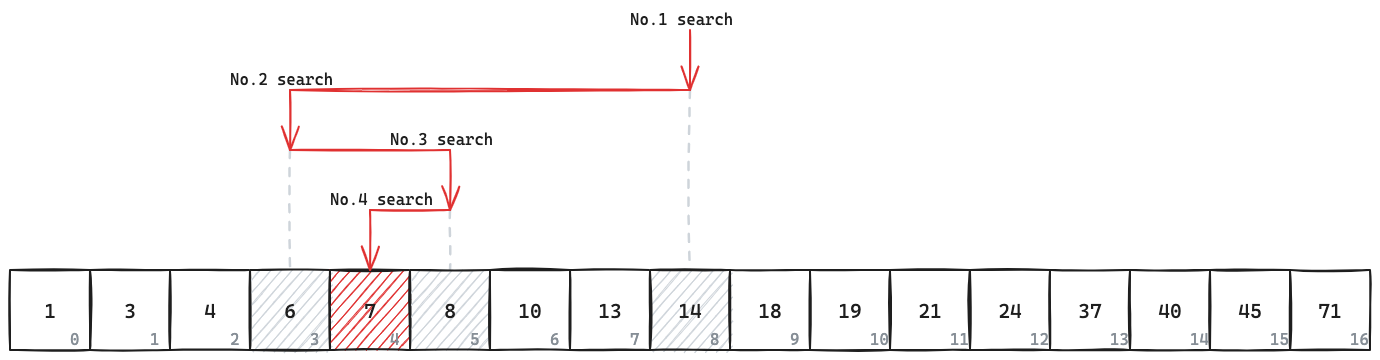
二分查找的最差时间复杂度是 $O(log\ n)$，空间复杂度是 $O(1)$。相比于最差时间复杂度为 $O(n)$ 的线性查找（Linear Search），二分查找执行更快、效率更高。相比于为快速查找量身定制的数据结构哈希表（Hash Table），二分查找的限制更少、应用更广。

二分查找有许多不同的变种版本，例如 Fractional Cascading 加速了二分查找在多个数组中对相同数值的搜索速度，有效解决了计算机几何以及其它领域中的一系列搜索相关问题；Exponential Search 扩展了二分查找算法，使其可以应用于无界列表。

二分查找的算法思想也衍生出了许多其它数据结构和算法，例如 Binary Search Tree 和 B-Tree。

初步实现

以 Java 语言为例，初步实现一个简单的二分查找算法，演示代码如下：

public int binarySearch(int[] arr, int low, int high, int key) {
    // 算法退出条件
    if (low > high) {
        return -1;
    }

     // 计算本次查找的中间值
    int mid = (low + high) / 2;

     // 二分查找的判断逻辑
    if (arr[mid] < key) {
        return binarySearch(arr, mid + 1, high, key);
    } else if (arr[mid] > key) {
        return binarySearch(arr, low, mid - 1, key);
    } else {
        return mid;
    }
}

依据文章开头的小提醒 review 上例代码，可以发现其中存在着的细节问题：

缺少参数校验

当输入参数 low 或 high 的数值小于零时，程序会存在逻辑错误。
递归查找的栈溢出

当查找的次数足够多时，程序会抛出 java.lang.StackOverflowError 异常。
中值计算的整型溢出

当查找的数组足够大时，直接使用 (low + high) / 2 计算二分查找过程中的中间数值，程序会存在整型数值溢出的问题。

正确实现

修复上述提及的三个问题，演示代码如下：

public int binarySearch(int[] arr, int low, int high, int key) {
    // 参数校验
    if (arr == null || arr.length == 0 || low < 0 || high < 0) {
        return -1;
    }

    while (true) {
        // 算法退出条件
        if (low > high) {
            return -1;
        }

        // 计算本次查找的中间值
        int mid = low + ((high - low) >>> 1);

        // 二分查找的判断逻辑
        if (arr[mid] < key) {
            low = mid + 1;
        } else if (arr[mid] > key) {
            high = mid - 1;
        } else {
            return mid;
        }
    }
}